定义和基本术语

结点的层次（深度）：从上往下数

结点的高度：从下往上数

结点的度：有几个孩子（分支）

树的高度（深度）：总共有几层

树的度：各结点的度的最大值

性质（常考）

常见考点 1： 结点数 = 总度数 + 1（总度数就是总边数）

常见考点 2： 度为 m 的树、m 查数的区别

度为 m 的树	m 叉树
任意结点的度≤m（最多 m 个孩子）	任意结点的度≤m（最多 m 个孩子）
至少有一个结点度 = m（有 m 个孩子）	允许所有结点的度都 < m
一定是非空树，至少有 m+1 个结点	可以是空树

常见考点 3： 度为 m 的树第 i 层最多有$m^{i-1}$ 个结点（$i\ge 1$），即 m 叉树第 i 层最多有$m^{i-1}$ 个结点

$$$$

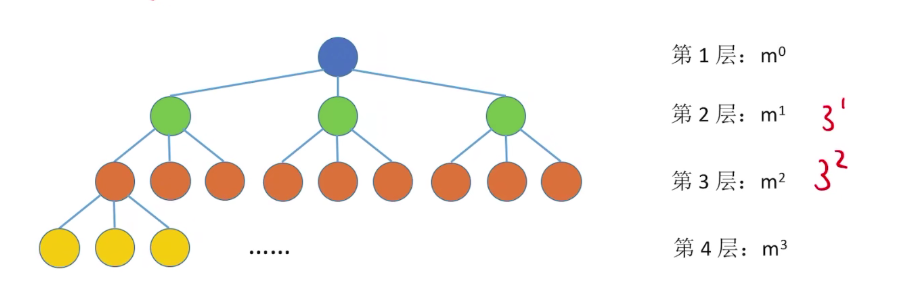
常见考点 4： 高度为 h 的 m 叉树至多有$\frac{m^h-1}{m-1}$ 个结点

$$$$

常见考点 5：

• 高度 h 的 m 叉树至少有 h 个结点
• 高度 h 度为 m 的树至少有 h + m - 1 个结点

常见考点 6： 具有 n 个结点的 m 叉树的最小高度为${\log }_m(n(m-1)+1)$

$$$$

二叉树

特点：

1. 每个结点至多只有两颗子树
2. 左右子树不能颠倒（二叉树是有序树）

满二叉树

一颗高度为 h，且含有$2^h-1$ 个结点的二叉树

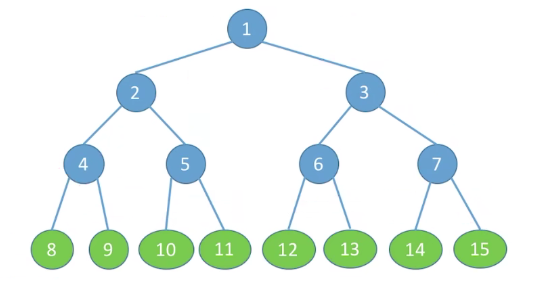
特点：

1. 只有最后一层有叶子结点
2. 不存在度为 1 的结点
3. 按层序从 1 开始编号，结点 i 的左孩子为 2i ，右孩子为 2i+1 ；结点 i 的父结点为$\lfloor i/2\rfloor$（如果有的话）

完全二叉树

当且仅当其每个结点都与高度为 h 的满二叉树中编号 1~n 的结点一一对应时，称为完全二叉树。

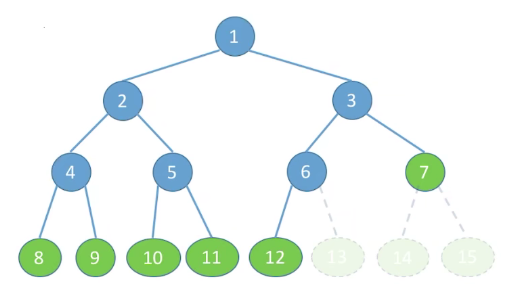
特点：

1. 只有最后两层可能有叶子结点
2. 最多只有一个度为 1 的结点（必须是左节点）
3. 【与满二叉树特点 3 相同】按层序从 1 开始编号，结点 i 的左孩子为 2i ，右孩子为 2i+1 ；结点 i 的父结点为$\lfloor i/2\rfloor$（如果有的话）
4. $i\le \lfloor n/2\rfloor$ 为分支结点，$i＞\lfloor n/2\rfloor$ 为叶子结点

二叉排序树

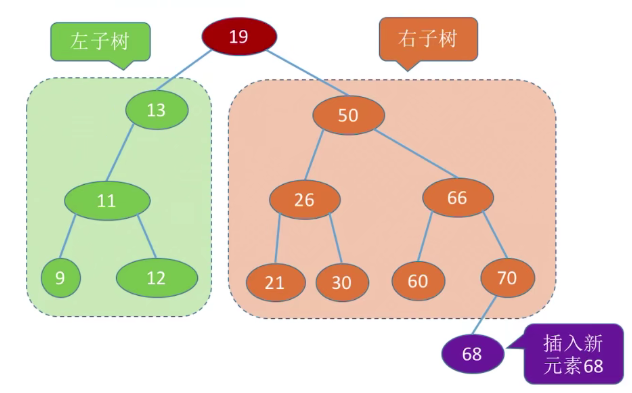
二叉排序树可用于元素的排序、搜索

左子树上所有结点的关键字均小于根结点的关键字；

右子树上所有结点的关键字均大于根结点的关键字。

左子树和右子树又各是一颗二叉排序树

中序遍历到的第一个元素，就是排序树最小的元素。

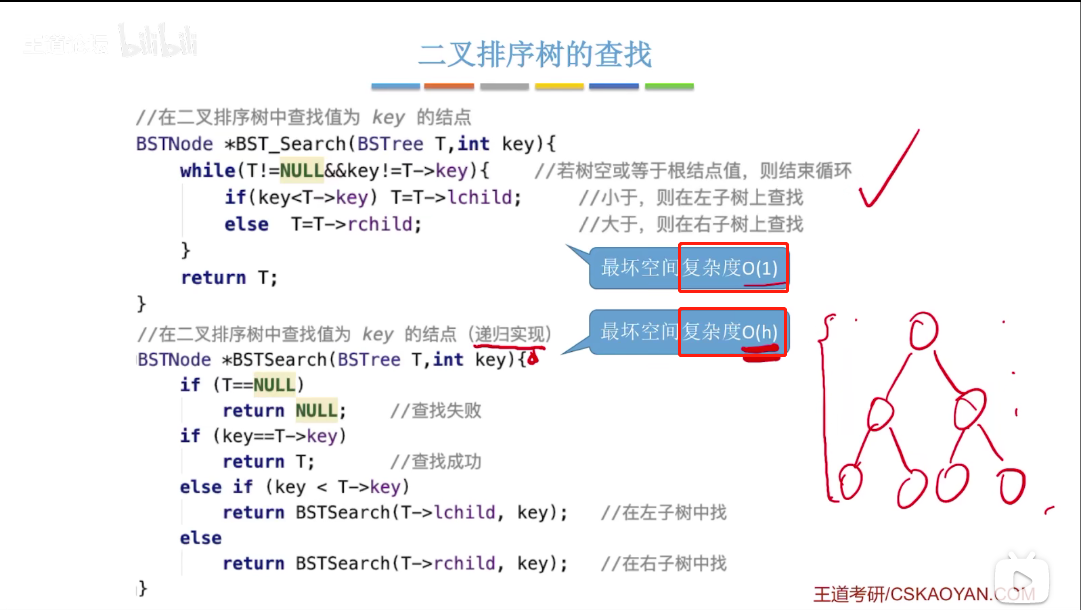
查找空间复杂度（栈内存）：

二叉排序树的删除

先搜索找到目标结点：

1. 若被删除结点 z 是叶结点，则直接删除，不会破坏二叉排序树的性质。
2. 若结点 z 只有一颗左子树或右子树，则让 z 的子树成为 z 父结点的子树，替代 z 的位置。
3. 若结点 z 有左、右两颗子树，则令 z 的中序遍历序列的直接后继（或直接前驱）替代 z，然后从二叉排序树中删去这个直接后继（或直接前驱），这样就转换成了第 1 种或第 2 种情况。

查找效率分析（缺点）

查找成功的平均查找长度（ASL）

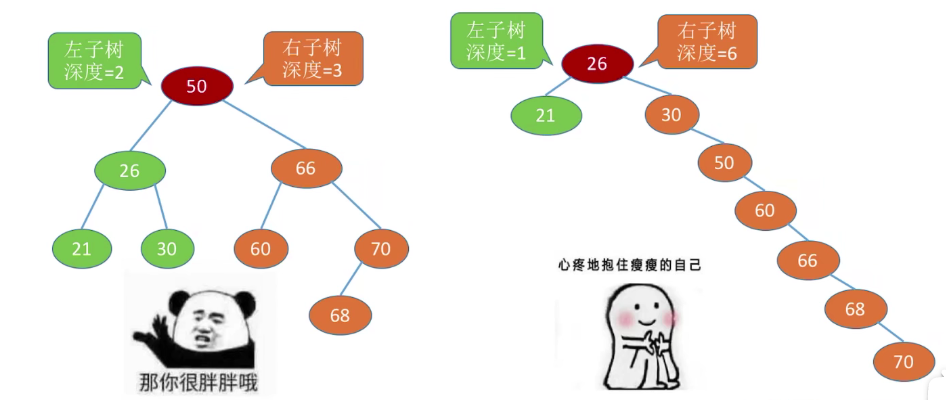
最好的情况：n 个结点的二叉树最小高度为$\lfloor lo{g}_{2}n\rfloor +1$，平均查找长度$O(lo{g}_{2}n)$

最坏的情况：每个结点只有一个分支，$\mathrm{树}\mathrm{高}h=\mathrm{结}\mathrm{点}\mathrm{数}n$，平均查找长度$O(n)$，即退化为链表

为了解决最坏的情况的问题，因此有了下面的平衡二叉树

平衡二叉树（AVL）

解决二叉排序树退化为链表，提高查询效率

概念

树上的任一结点的左子树和右子树的深度之差不超过 1。

$$\mathrm{结}\mathrm{点}\mathrm{的}\mathrm{平}\mathrm{衡}\mathrm{因}\mathrm{子}=\mathrm{左}\mathrm{子}\mathrm{树}\mathrm{高}-\mathrm{右}\mathrm{子}\mathrm{树}\mathrm{高}（\mathrm{只}\mathrm{可}\mathrm{能}\mathrm{是}-1、0、1）$$

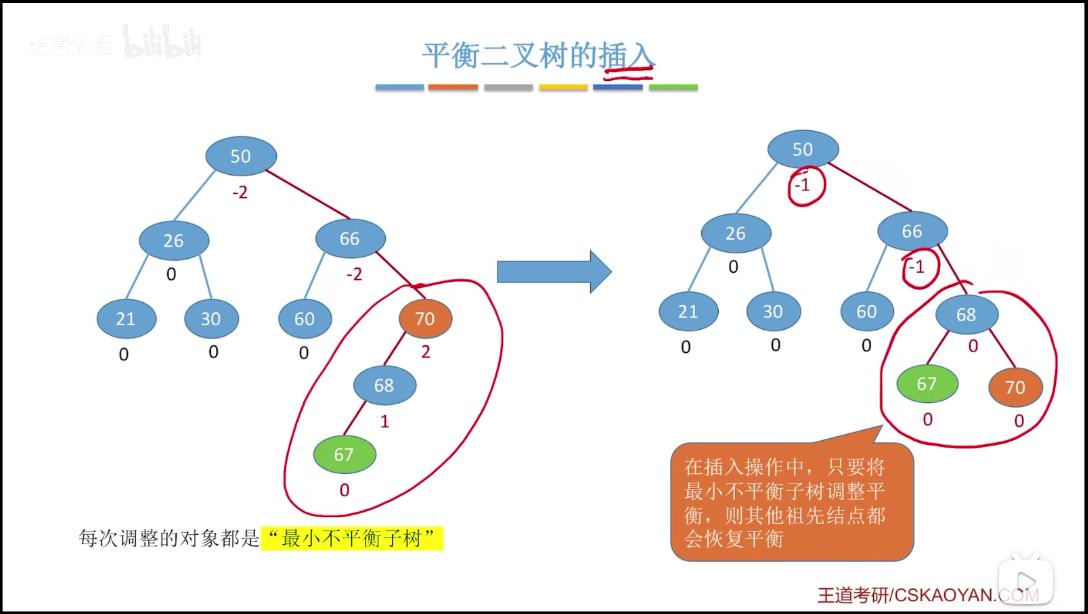
插入

在插入操作中，只要将最小不平衡子树调整平衡，则其他祖先结点都会恢复平衡。

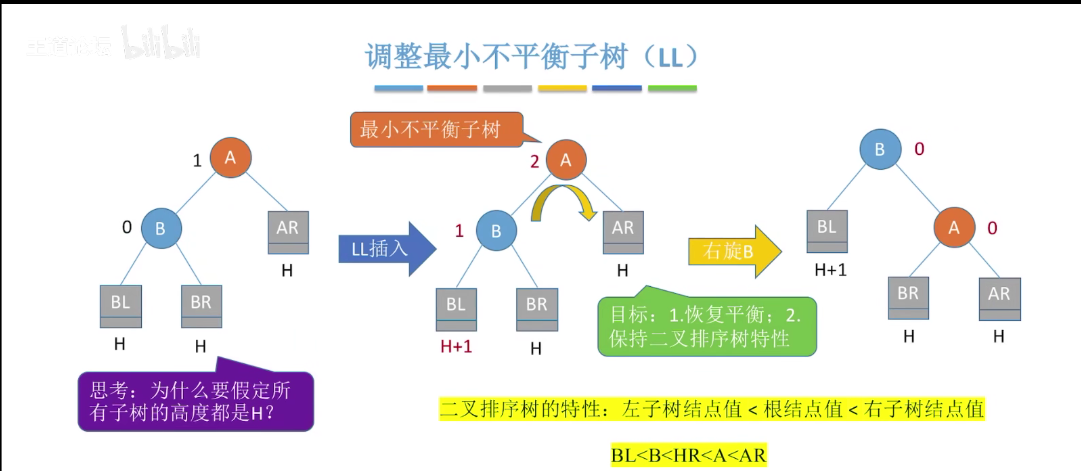
调整最小不平衡子树（LL）

1）LL 平衡旋转（右单旋转）。由于在结点 A 的左孩子（L）的左子树（L）上插入了新结点，A 的平衡因子由 1 增至 2，导致以 A 为根的子树失去平衡，需要一次向右的旋转操作。将 A 的左孩子 B 向右上旋转替代 A 称为根结点，将 A 结点向右下旋转称为 B 的右子树的根结点，而 B 的原右子树则作为 A 结点的左子树。

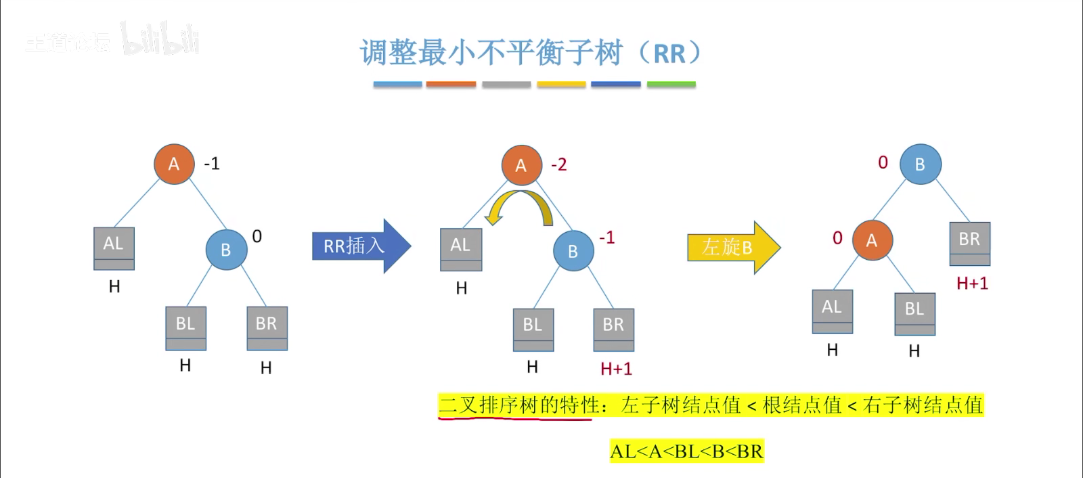
2）RR 平衡旋转（左单旋转）。由于在结点 A 的右孩子（R）的右子树（R）上插入了新结点，A 的平衡因子由 - 1 减至 - 2，导致以 A 为根的子树失去平衡，需要一次向左的旋转操作。将 A 的右孩子 B 向左上旋转代替 A 称为根节点，将 A 结点向左下旋转称为 B 的左子树的根节点，而 B 的左子树则作为 A 结点的右子树。

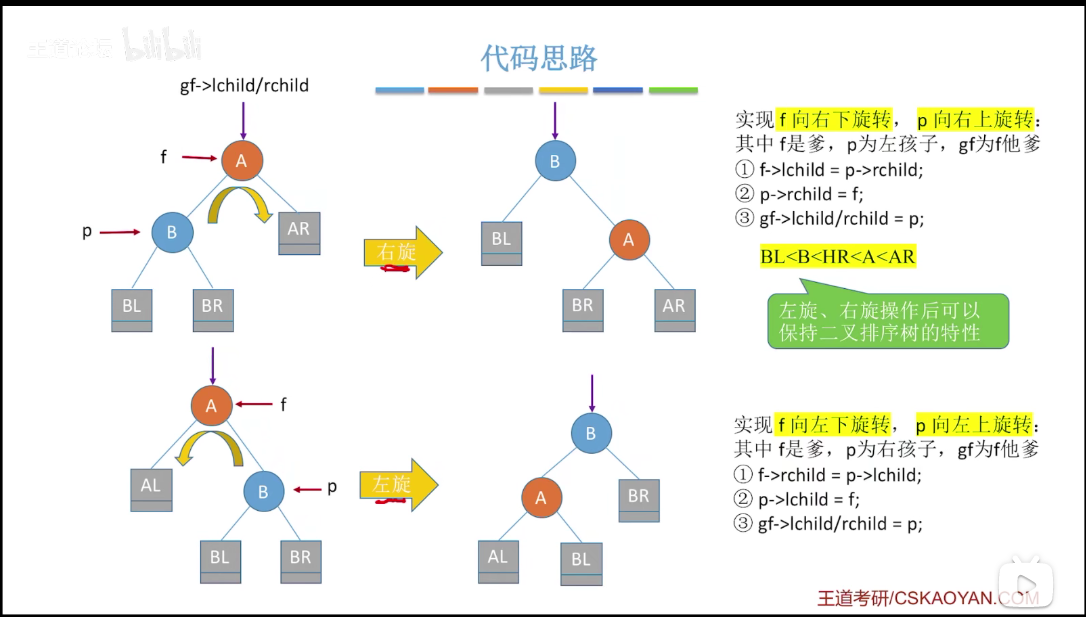
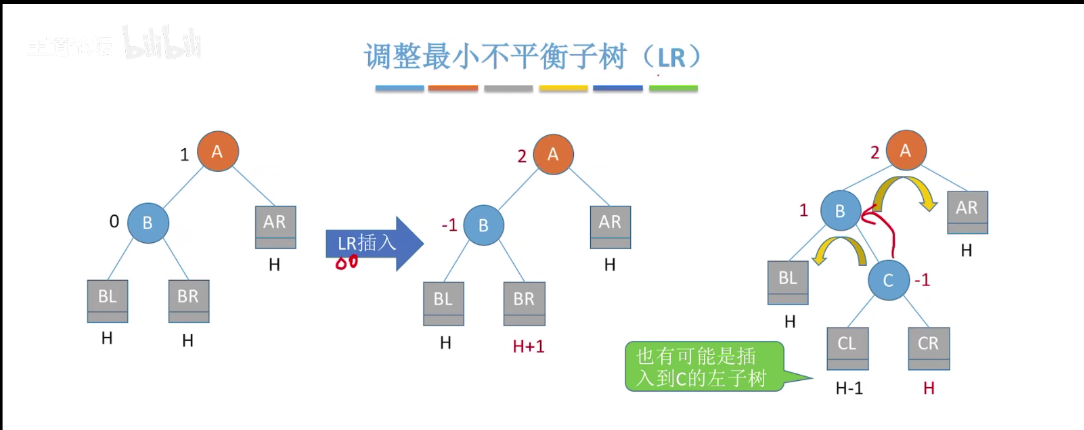
3）LR 平衡旋转（先左后右双旋转）。由于在 A 的左孩子（L）的右子树（R）上插入新结点，A 的平衡因子由 1 增至 2，导致以 A 为根的子树失去平衡，需要进行两次旋转操作，先左旋转后右旋转，先将 A 结点的左孩子 B 的右子树的根结点 C 向左上旋提升到 B 结点的位置，然后再把该 C 结点向右上旋转提升到 A 结点的位置。

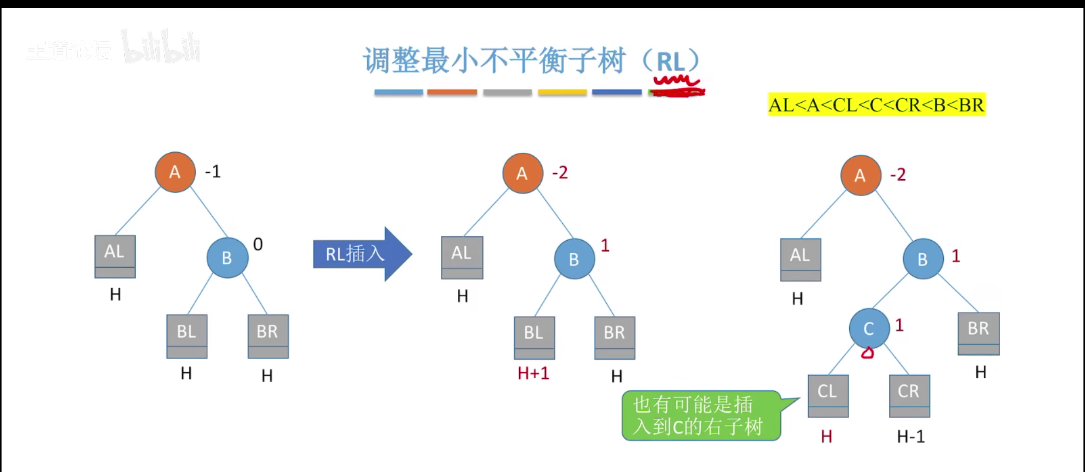
4）RL 平衡旋转（先右后左双旋转）。由于在 A 的右孩子（R）的左孩子（L）上插入新结点，A 的平衡因子由 - 1 减至 - 2，导致以 A 为根的子树失去平衡，需要进行两次旋转操作，先右旋转后左旋转。先将 A 结点的右孩子 B 的左子树的根节点 C 向右上旋转提升至 B 结点的位置，然后再把该 C 结点向左旋转提升到 A 结点的位置。

查找效率分析

最大深度：$O(lo{g}_{2}n)$（有 n 个结点）

平均查找长度：$O(lo{g}_{2}n)$

缺点

插入效率低

为了保证 “平衡”，AVL 树几乎每一次插入都需要进行调整，提高了查询效率的同时，也降低了插入效率。

为了在插入与查询效率效率间得到一个平衡，延伸出了 “红黑树” 的数据结构（在「查找」章节讲到）。

二叉树的常考性质

常见考点 1：设非空二叉树中度为 0、1 和 2 的结点个数为 n0、n1 和 n2，则 n0=n2+1（叶子结点比二分支结点多一个）

n0：叶子结点

常见考点 2：二叉树第 i 层至多有$2^{i-1}$ 个结点（i≥1）

常见考点 3：高度为 h 的二叉树至多有$2^h-1$ 个结点（满二叉树）

完全二叉树的常考性质

常见考点 1：具有 n 个 (n>0) 结点的完全二叉树的高度 h 为$\lceil lo{g}_2(n+1)\rceil$ 或$\lfloor lo{g}_{2}n\rfloor +1$

常见考点 2：对于完全二叉树，可以由结点数 n 推出度为 0、1 和 2 的结点个数为$n_0$、$n_1$ 和$n_2$。

完全二叉树最多只有一个度为 1 的节点，即$n_1=0\mathrm{或}1$

$n_0=n_2+1$ 即 $n_0+n_2$ 一定是奇数

若完全二叉树有$2k$ 个 (偶数) 个结点，则必有$n_1=1，n_0=k，n_2=k-1$

若完全二叉树有$2k-1$ 个 (奇数) 个结点，必有$n_1=0，n_0=k，n_2=k-1$

二叉树的顺序存储

顺序存储只适合完全二叉树

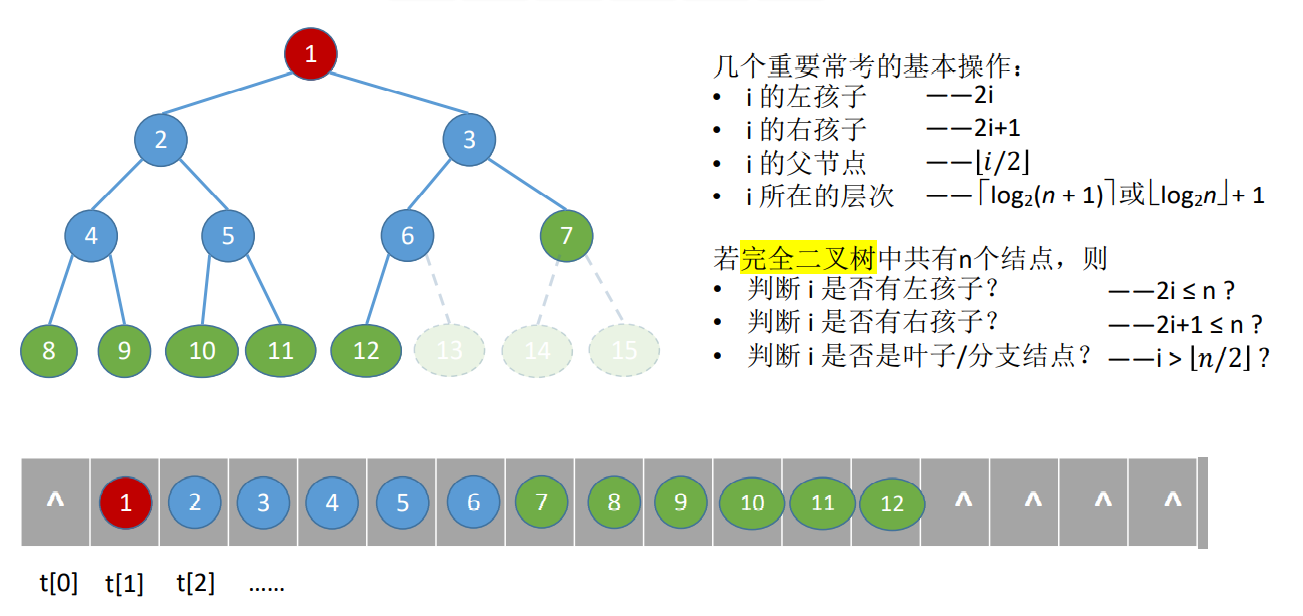
二叉树的链式存储

n 个结点的二叉链表共有 n+1 个空链域（可以用于构造线索二叉树）

二叉树的遍历

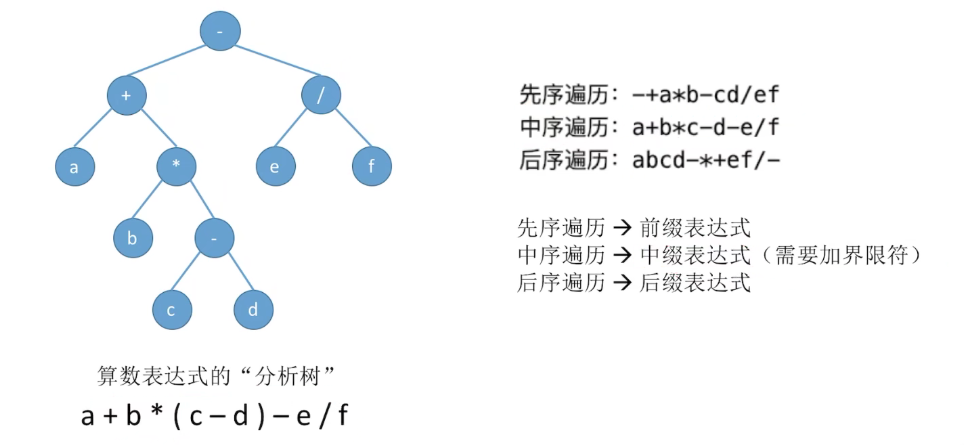
先序遍历

pubilc void PreOrder(BiTree T){
    if(T != null){
        system.out.println(T.val); // 打印当前结点的值
        this.PreOrder(T.leftChild); // 递归遍历左子树
        this.PreOrder(T.rightChild); // 递归遍历右子树
    }
}

中序遍历

pubilc void InOrder(BiTree T){
    if(T != null){
        this.PreOrder(T.leftChild); // 递归遍历左子树
        system.out.println(T.val); // 打印当前结点的值
        this.PreOrder(T.rightChild); // 递归遍历右子树
    }
}

后序遍历

pubilc void PostOrder(BiTree T){
    if(T != null){
        this.PreOrder(T.leftChild); // 递归遍历左子树
        this.PreOrder(T.rightChild); // 递归遍历右子树
        system.out.println(T.val); // 打印当前结点的值
    }
}

求二叉树的深度

当前结点的深度 = $Max(\mathrm{左}\mathrm{子}\mathrm{树}\mathrm{深}\mathrm{度},\mathrm{右}\mathrm{子}\mathrm{树}\mathrm{深}\mathrm{度})+1$

public int treeDepth(BiTree T){
    if(T == null){
        return 0;
    }
    
    int l = this.treeDepth(T.leftChild);
    int r = this.treeDepth(T.rightChild);
    // 树的深度 = Max(左子树深度,右子树深度) + 1
    return l>r ? l+1 : r+1;
    
}

二叉树的层次遍历

算法思想：

1. 初始化一个辅助队列
2. 根节点入队
3. 若队列非空，则队头结点出队，访问该结点，并将其左、右孩子插入队尾（如果有的话）
4. 重复③直至队列为空

public LevelOrder(BiTree T){
    Queue<BiTree> queue = new LinkedList<>(); // 初始化辅助队列
    queue.add(T); // 将根节点入队
    
    while(queue.peek() != null){  // 队列不为空则循环
        T = queue.poll(); // 出队队头元素
        
        system.out.println(T.val); // 访问出栈结点
        
        if(T.leftChild != null){
            queue.add(T.leftChild); // 左孩子结点入队
        }
        
        if(T.rightChild != null){
            queue.add(T.rightChild); // 右孩子结点入队
        }
        
    }
}

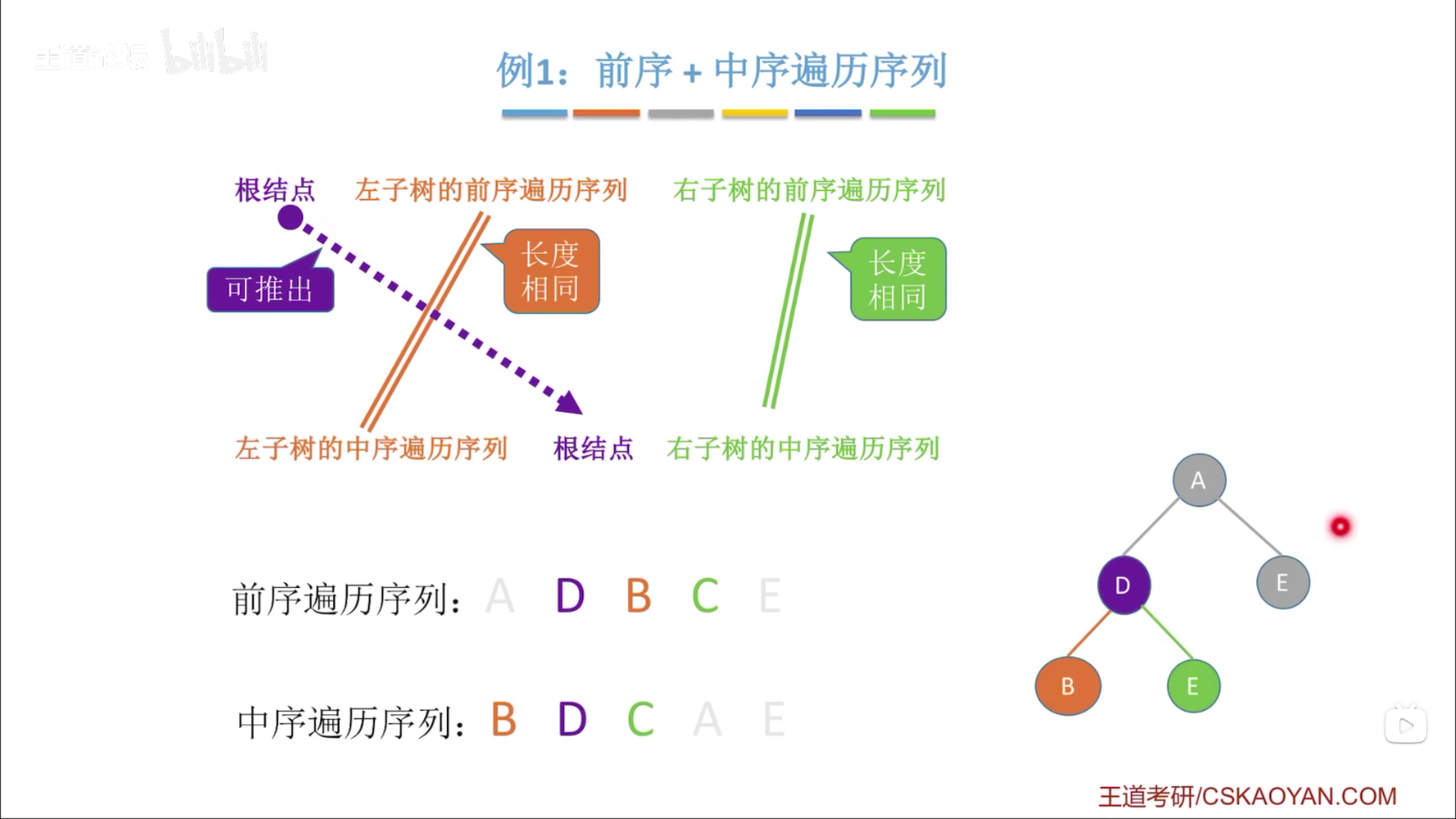
由遍历序列构建二叉树

由两种遍历可确定一颗二叉树，其中一种遍历必须使中序遍历。

前序遍历： 根节点 + 左子树的前序遍历序列 + 右子树的前序遍历序列

中序遍历： 左子树的中序遍历 + 根节点 + 右子树的中序遍历序列

后续遍历： 左子树的后序遍历序列 + 右子树的后序遍历序列 + 根节点

层序遍历： 根节点 + 左子树的根节点 + 右子树的根节点 + ...

线索二叉树

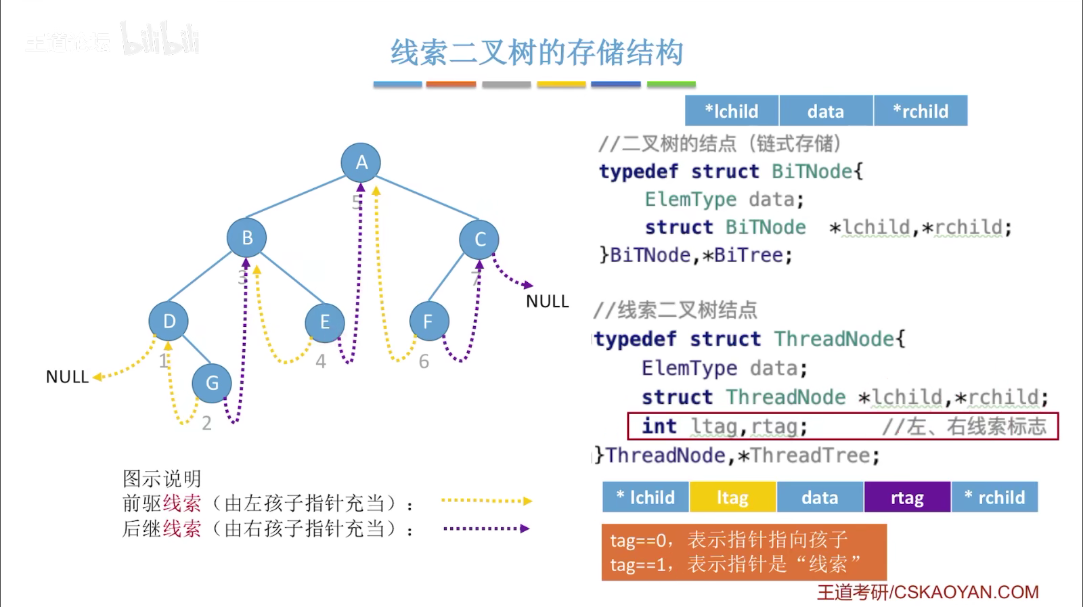
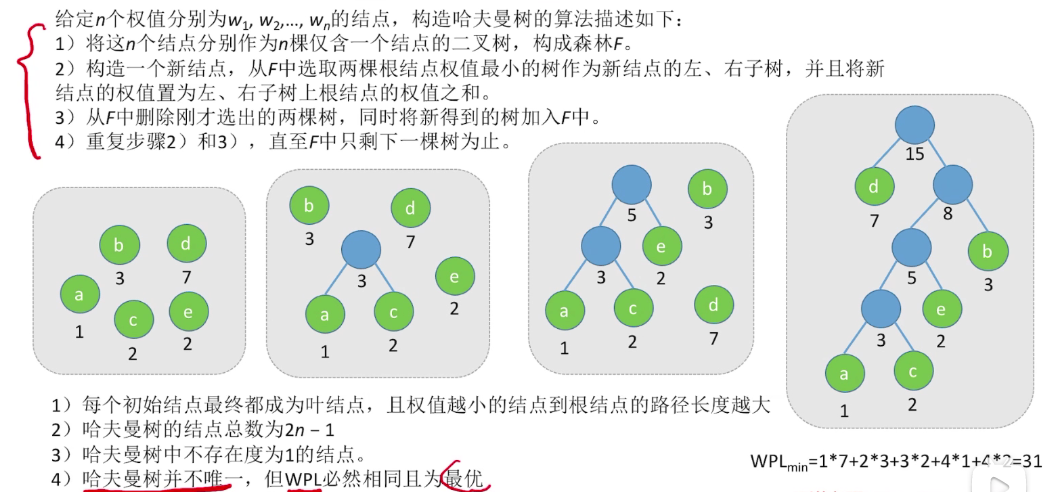
哈夫曼树

定义

在含有 n 个带权叶结点的二叉树中，其中带权路径长度（WPL）最小的二叉树称为哈夫曼树，也称最优二叉树

带权路径长度（WPL）：树中所有叶子结点的带权路径长度之和

构造

每次选最小的两个结点